Dynamic Programming

Basic: Fibonacci Sequence

Dynamic programming 적용 가능 조건 세 가지!

  • Problem이 subproblem으로 나뉠 수 있어야 하고,
  • Subproblem의 결과를 이용해 상위 subproblem을 풀 수 있어야 하고,
  • 같은 subproblem을 여러번 반복해서 풀어야할 때
    • Memoization을 이용!

피보나치 수열을 생각해보자.

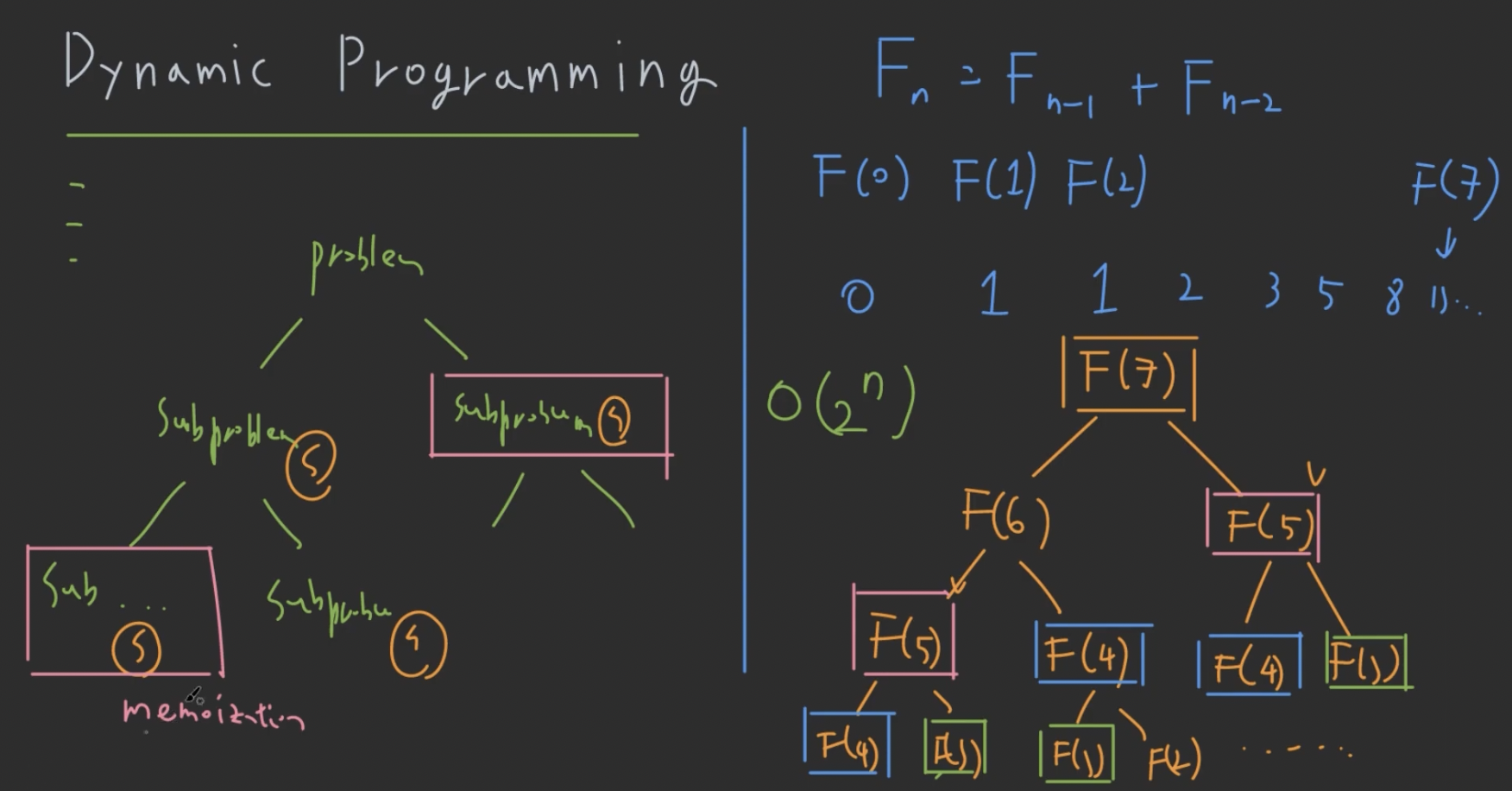
  • $F_n = F_{n-1} + F_{n-2}$
  • n이 하나 줄어들면서 다음 층이 생기니깐
  • $O(2^n)$ complexity로 너무 비쌈
  • 근데 dynamic programming 적용가능 조건 만족하니깐, O(n)으로 줄어듬.

Tip: Recursive dynamic programming의 문제:

  • Top-down vs Bottom-up
    • 맨 위에서부터 문제를 쪼개면서 해결하려고 하기 때문에 Top-down 방식이라고도 하는데,
    • Recusion을 너무 많이하면,
    • Call stack이 너무 많이 쌓여서 “maximum recursion depth”를 초과한다는 에러 발생할 수 있음
    • 그니깐… Bottom-up 방식(배열의 맨 아래부터 하나씩 결과값을 채워나가는 방식)이 더 안전함.
  • Array size
    • $F_n$ 구하려면 n+1 개 원소 갖는 배열을 채워나가는게 자연스러운 방법이긴 하지만,
    • $Fn$을 위해서 $F_{n-1}$, $F_{n-2}$ 두 숫자만 있으면 되니깐,
    • 딱 2~3개 원소만 있는 배열로도 충분하긴 함.

Climbing Stairs

높이 n의 계단이 있는데,

  • 예를 들어 한번에 한 칸 혹은 두 칸 올라갈 수 있을 때,
  • n번째 계단가지 올라갈 수 있는 경우의 수
  • LeetCode70. Climbing Stairs

풀이 방법

  • Recursion relation: $F_n = F_{n-1} + F_{n-2}$
  • Fibonacci 수열과 똑같은 점화식
  • 하지만 Fibonacci 수열과 초기값이 다른데,
    • $F_1 = 1$ (한 칸 올라가면 됨)
    • $F_2 = 2$ (한 칸 두번 올라가거나, 두 칸 한번에 올라가면 됨)
  • Bottom-up dynamic programming 해서 배열을 아래부터 채워나가면 됨.

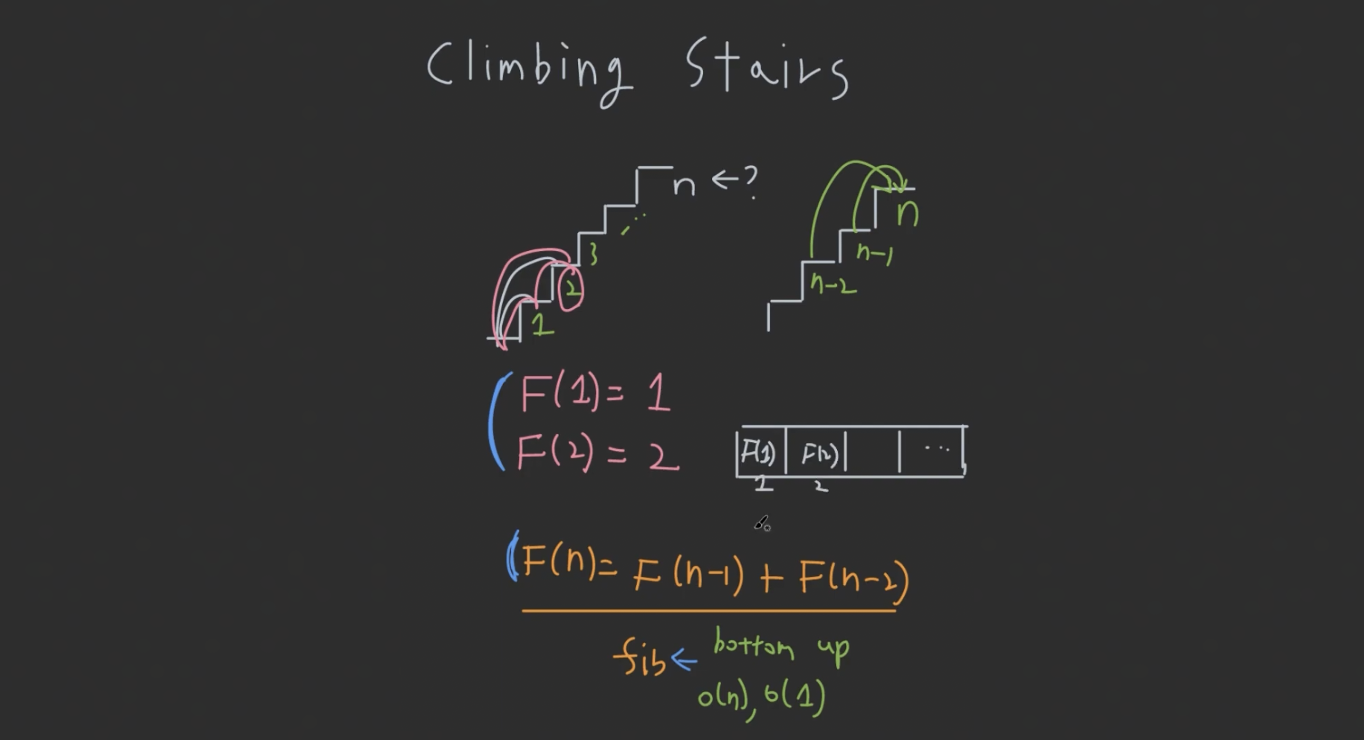
Min Cost Climbing Stairs

각 계단마다 올라타는데 비용이 드는 경우,

  • 예를 들어 4칸 계단을 올라가는 1~3번째 계단의 비용이 $[10, 20, 30]$ 인 경우,
  • 마찬가지로 한번에 한 칸 혹은 두 칸만 올라갈 수 있으면,
  • Min cost 방법은 2번째 계단 들려서 4번째 칸 가는 20-cost 경로가 정답.
  • LeetCode746. Min Cost Climbing Stairs

풀이 방법

  • 계단의 첫번째 칸은 index를 0이라고 할 때
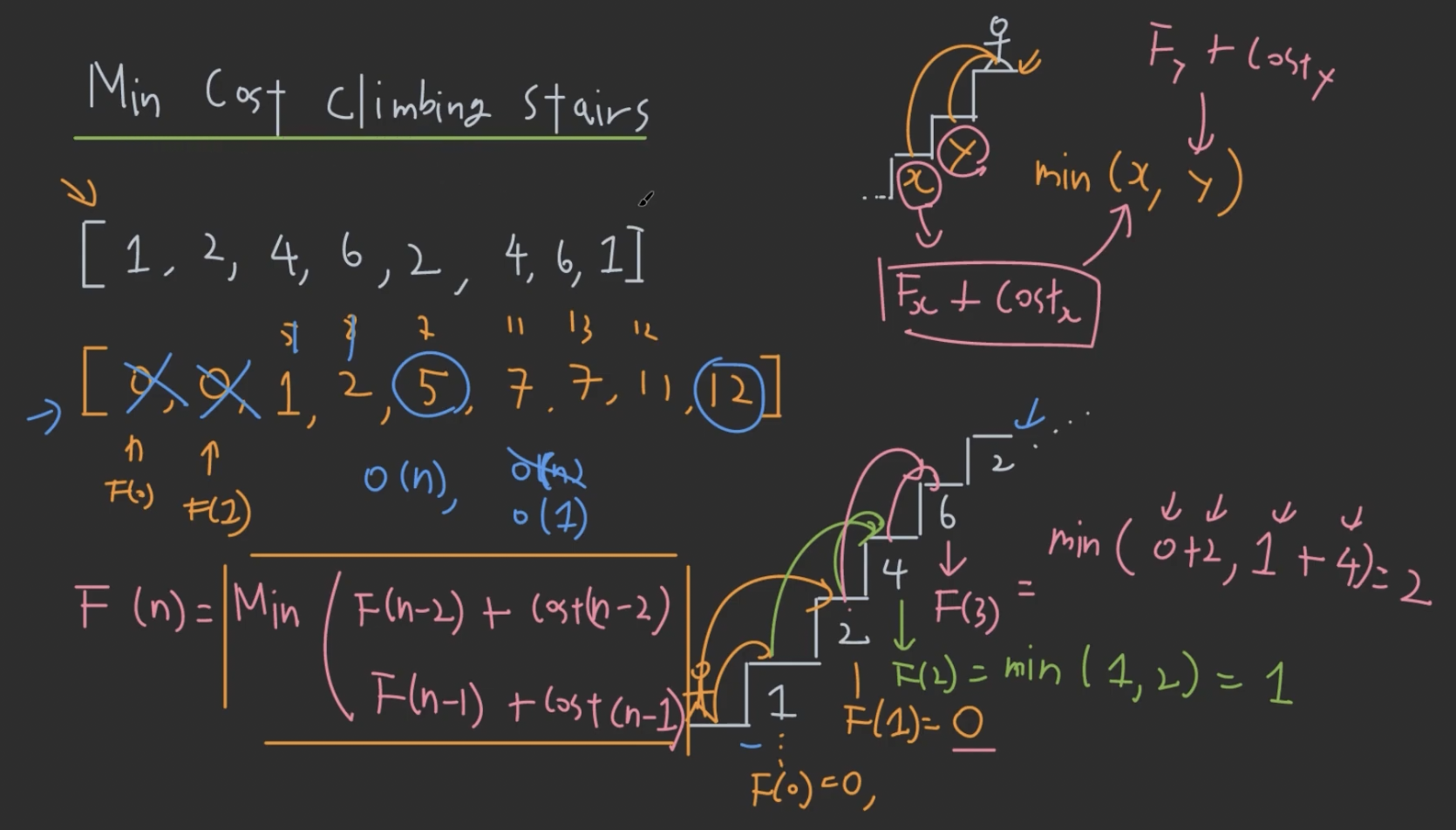
  • 비용: $[1,2,4,6,2,4,6,1]$
  • $F_0 = 0$ : cost 없는 시작점에서 한 칸 올라가면 됨.
  • $F_1 = 0$ : cost 없는 시작점에서 두 칸 올라가면 됨.
  • $F_i = min(F_{i-1}+cost[i-1],F_{i-2}+cost[i-2])$
    • $i$ 번째 칸으로 도착하기 위해서
    • 한 칸 오른 경우 비용 $F_{i-1}+cost[i-1]$
    • 두 칸 오른 경우 비용 $F_{i-2}+cost[i-2])$
    • 둘 중에 작은 값을 선택하면 됨

Minimum Path Sum

4x4 매트릭스에 각 칸을 지나가는데 드는 비용이 적혀있음

  • 한 칸씩 움직일 수 있는데,
  • 길을 가는 방법은 오른쪽 또는 아래쪽으로만 이동가능
  • Min Cost Climbing Stairs 문제를 2D로 바꾼 문제에 불과함
  • LeetCode64. Minimum Path Sum

풀이 방법

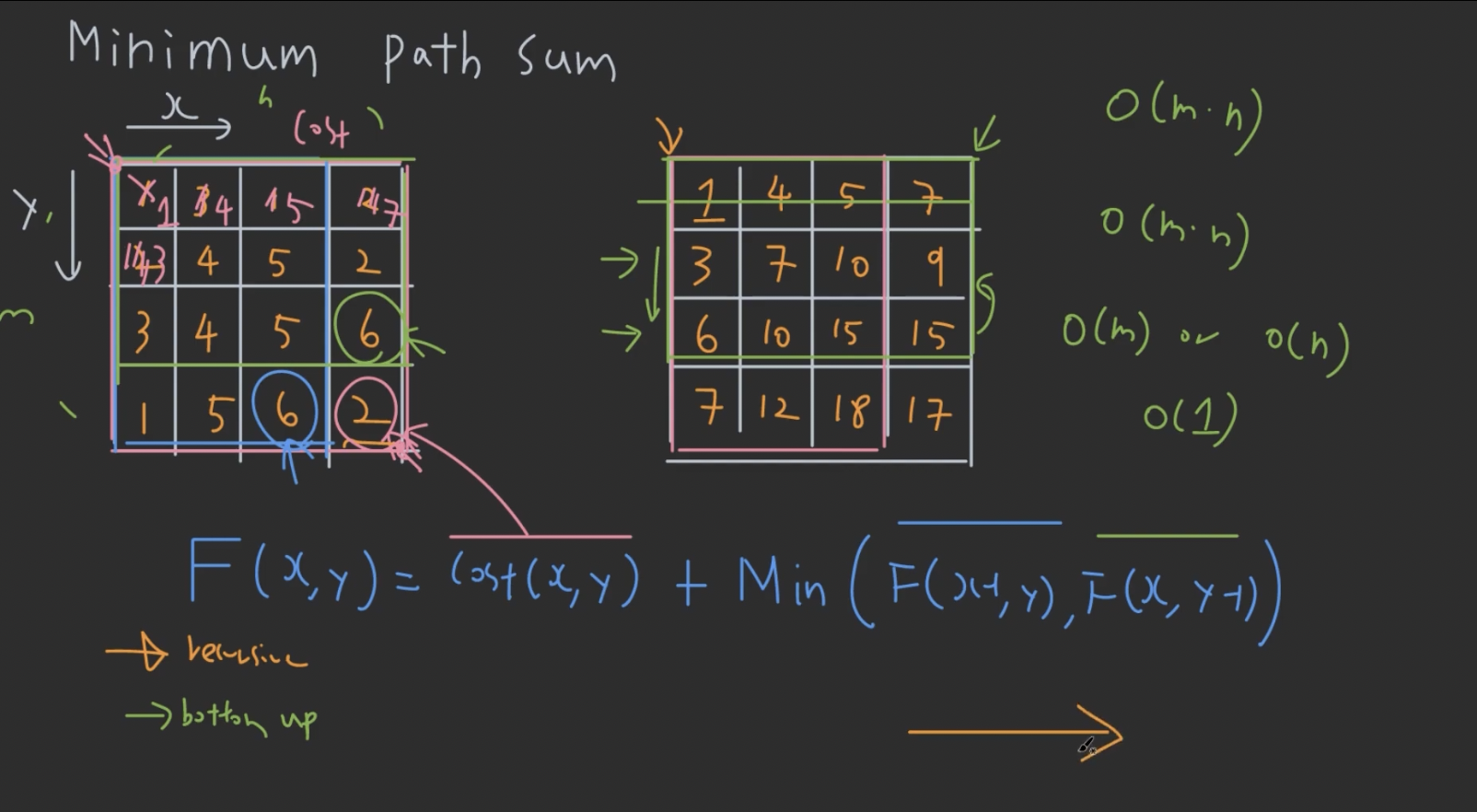
  • $F(x,y) = cost(x,y) + min(F(x-1,y),F(x,y-1))$
  • 입력으로 주어진 각 칸의 cost table과 같은 모양을 갖는
  • 최종 cost table을 채워나가면 됨.
  • MxN 매트릭스의 경우, O(mn) 시간복잡도, O(mn) 공간복잡도 가짐
  • Space optimization:
    • 한 row를 완성하고 다음 row를 완성해도 되니깐 O(n) 공간만 필요
    • 한 col를 완성하고 다음 col를 완성해도 되니깐 O(min(n,m)) 공간만 필요
    • 입력 테이블을 그대로 활용해도 되니간 O(1)에 해결

Min Coin Change

목표 금액 만들기 위해 필요한 동전의 최소 갯수 구하기

  • 입력으로 목표 금액과 동전 종류가 주어짐
  • 목표금액 못 만들면 -1 리턴
  • LeetCode322. Coin Change

풀이 방법

  • $F(n) = min(F(n-2) + F(n-3) + F(n-5)) + 1$
  • Bottom-up이 top-down보다 좋으니깐, 배열 채워가면서 문제 풀자

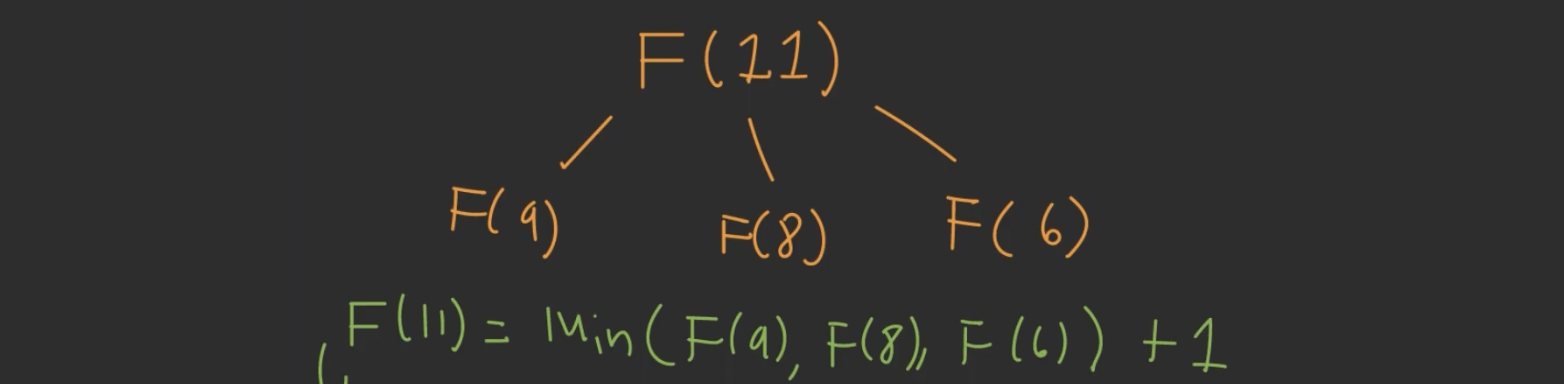
Decode ways

인코딩된 숫자를 디코드하는 방법의 갯수 구하기

  • A = 1, B = 2, C =3, …
  • V = 22, W = 23, …Z = 26 으로 인코딩 될 때
  • [2,2,3]은
  • BBC, BW, VC
  • 이렇게 3가지로 decode 될 수 있음.
  • LeetCode91. Decode ways

풀이 방법

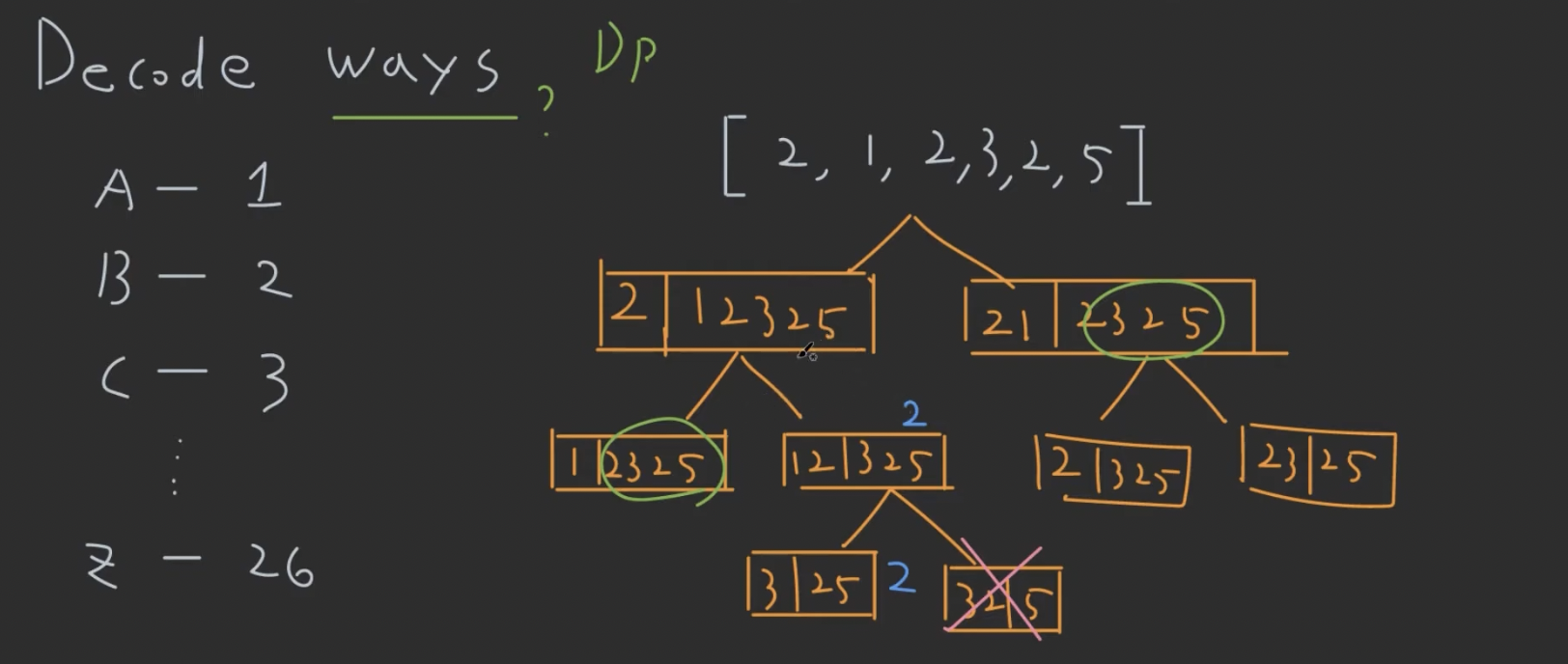
  • [2,1,2,3,2,5] 같은 배열을 decoding 하는 경우의 수 셀 때,
  • 기본 problem 은 첫번째 원소와 나머지, 첫 두개의 원소와 나머지, 이렇게 두가지 sub-problem으로 나눌 수 있다.
  • 각 Sub-problem은 또 다시 두가지 sub-problem으로 나눌 수 있다.
  • Sub-problem 의 결과를 memoization해서 Dynamic programming 으로 풀면 됨.

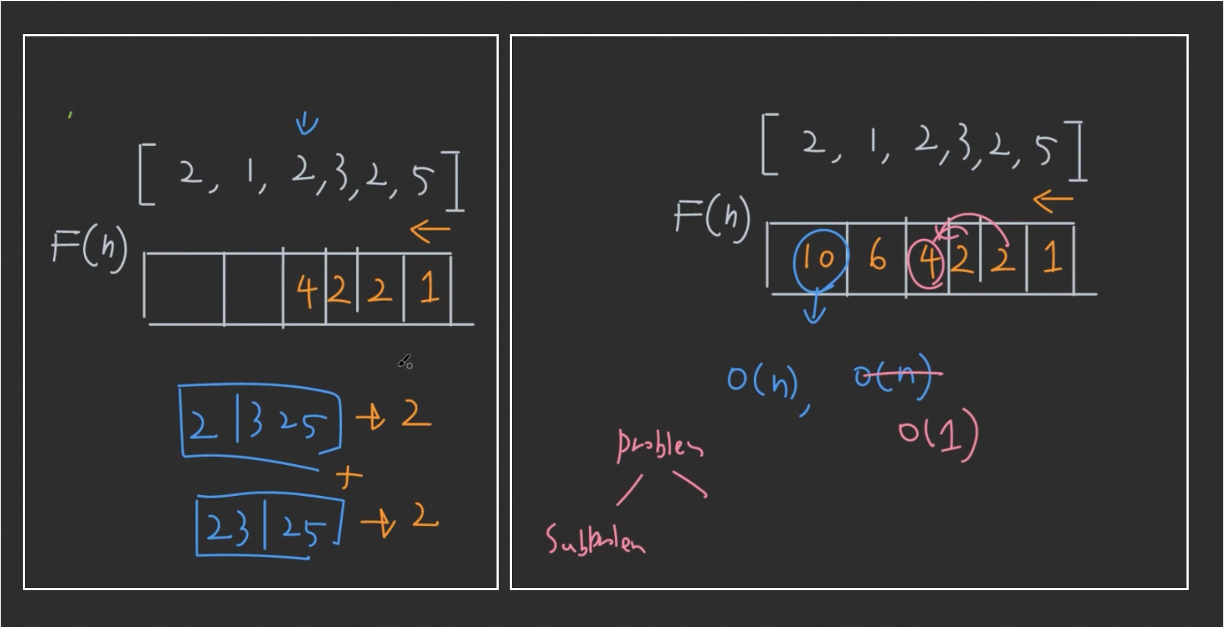
  • Bottom-up으로 풀고 싶으면, 맨 뒤의 원소 부터 앞 방향으로 진행
  • O(n) time, O(n) space $\rightarrow$ 맨 앞 두 칸만 있으면 되니깐 O(1) space

Maximum Subarray

Array 받아서, 최대합 주는 Subarray 찾기

풀이 방법

  • Brute force:
    • L/R-pointer 잡고 그 내부의 subarray element 다 더하기 $\rightarrow$ $O(n^3)$
    • R-pointer를 L-pointer로부터 오른쪽으로 가면서 temporary sum을 업데이트하는 방식 $\rightarrow$ $O(n^2)$
  • 배열 문제인가?
    • 배열이 주어지기 때문에, sorting을 하는 등 배열의 전형적인 풀이 방법을 생각하게 되는데,
    • 이 문제를 optimization으로 보려고 하고, sub-problem 으로 쪼개보려고 하면, dynamic problem으로 볼 수 있게 됨.
  • Subproblem으로 나누려면?
    • n개 원소로 이뤄진 배열 A(n)의 maximum subarray S(n)를 알고 있다고 해보자.
    • 1개 원소(x)를 뒤에 추가해서 만든 배열A(n+1)의 maximum subarray S(n+1) 은 …
    • S(n), {S(n), 혹은 S(n) 의 뒷부분}.append(x) 중 하나일 것.
    • 그런데 S(n)이 맨 뒤 원소와 연결이 안되어 있으면,
    • 새로 추가된 원소 x랑 S(n)이 연결이 안되어 있어서, S(n)에 x를 추가한 새로운 subarray를 테스트 할 수 없음. (중간이 끊어지면 subarray가 아님!)
    • 그러면, sub-probelm으로 잘 안나눠지는 문제가 생김
    • 해결책: 맨 뒤 원소가 포함되지 않은 S(n)은 subproblem의 solution에서 배제시켜버리자.
  • Subproblem을 나누기 쉽게 문제를 재정의 하면,
    • Bottom-up으로 문제 풀면서,
    • Max subarray with the last element, 즉 마지막 원소를 포함한 max subarray를 구하도록 sub-문제를 재정의하면,
    • {S(n), 혹은 S(n) 의 뒷부분}.append(x) 으로 가능한 경우가 줄어들게 되서, recursion relation을 만들 수 있음.
  • 구체적 풀이 방법
    • 기록할 배열:
      • 주어진 배열 $In(n)$
      • Subarray 최대합 $maxVal(n)$
      • Max subarray의 시작 index 적은 $StartIdx(n)$
    • Recursion relation
      • $maxVal(i) =$ $max(In(i), In(i)+maxVal(i-1))$
    • O(n) time, O(n) space $\rightarrow$ 바로 앞 maxVal 값만 필요하니깐, O(1) space 로 최적화 가능.

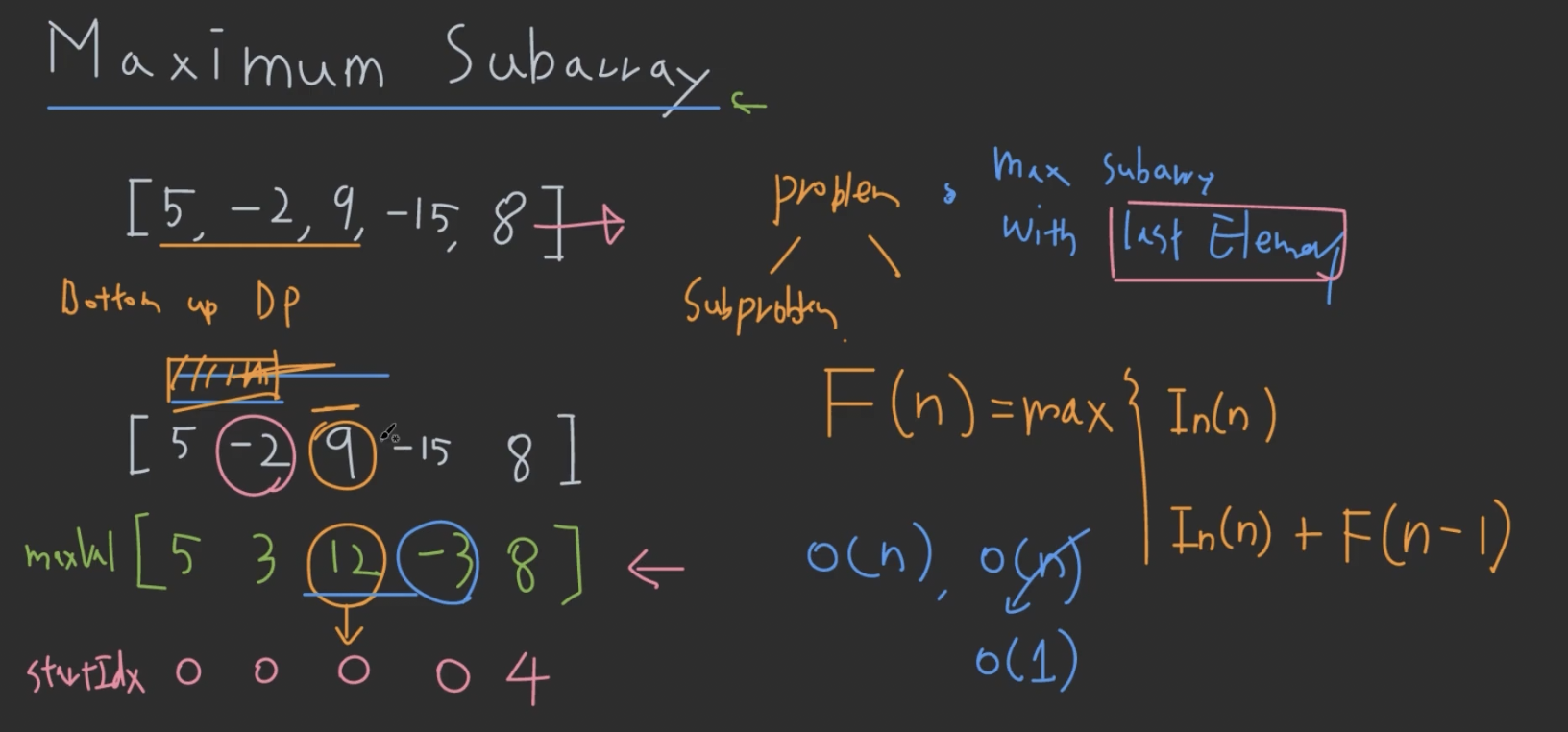
Maximum Product Subarray

주어진 배열에서, 곱한게 최대가 되는 subarray 찾기

풀이 방법

  • Maximum subarray 문제에서 푼 방법 활용
    • Sub-problem 정의할 때, 마지막 element를 포함하는 maximum subarray 를 리턴하도록 하면, 상위 문제 풀 때 subarray가 연결되도록 할 수 있음
  • 이번 문제의 차이점은, sum이 product로 바뀌었음.
    • 따라서, 새로운 원소가 추가된 배열의 최대곱은,
    • 추가 전 최대곱 뿐 아니라, 최소곱까지 기억해놨다가
    • 새로운 숫자가 양수면, 이전 최대곱과 곱해서 새로운 최대곱 구하고,
    • 새로운 숫자가 음수면, 이전 최곱과 곱해서 새로운 최대곱 구해서,
    • 더 큰 값 찾아야 함.
  • 즉, 점화식이 하나만 있는게 아니라, 두 개의 점화식이 교차됨 !

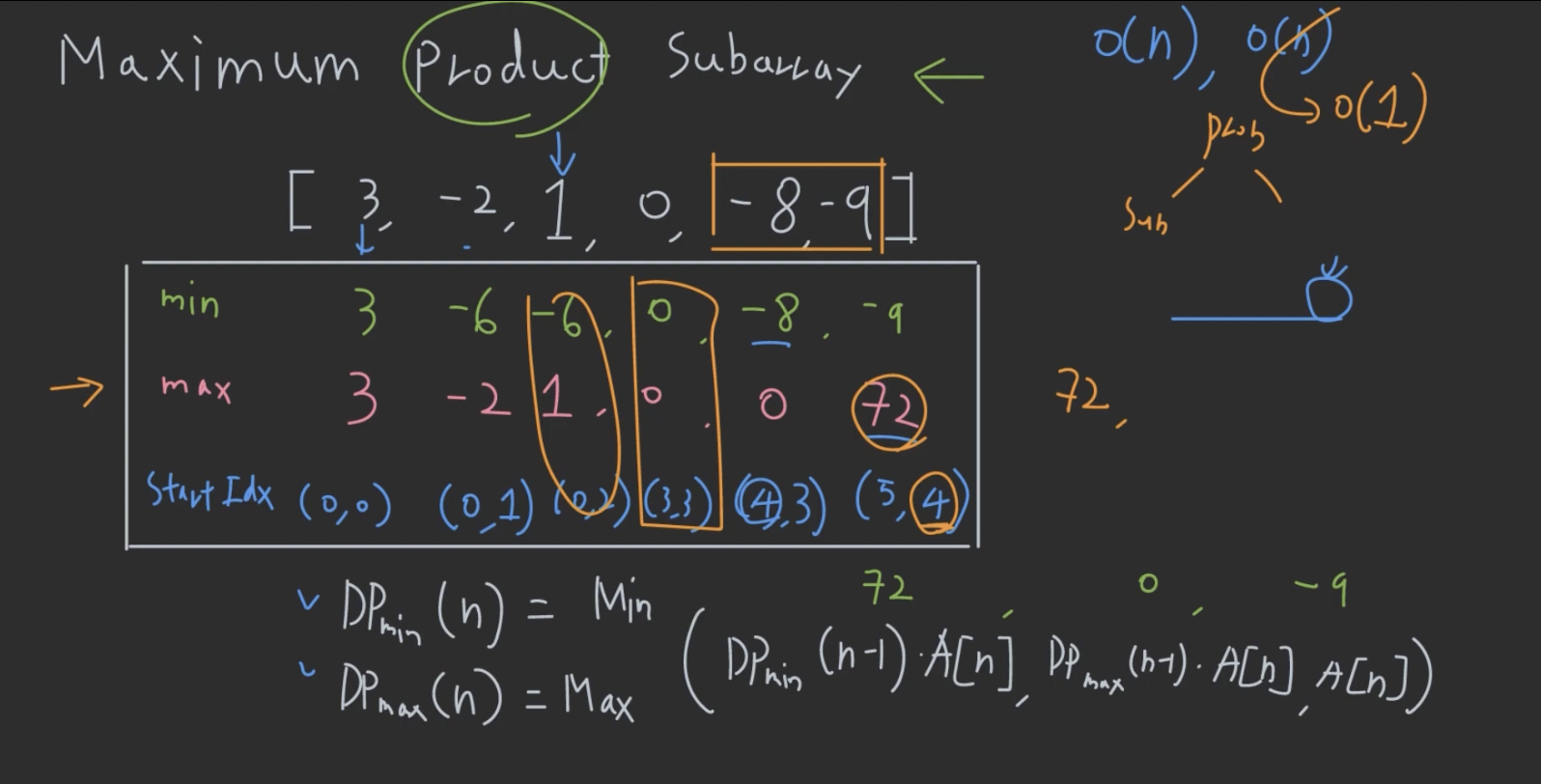
Longest Palindromic Substring

주어진 문자열에서 가장 긴 palindromic 성질 갖는 substring 리턴하기

풀이 방법

  • L/R 포인터 잡아서 만든 substring이 palindromic인지 체크 $\rightarrow$ $O(n^3)$
  • M 포인터 잡아서 양방향 동시 체크하면서 palindrom 아니면 M 포인터 이동 $\rightarrow$ $O(n^2)$
    • 짝수 substring, 홀수 substring 경우 모두 가능하므로 두 가지 경우 모두 체크
  • (m, n) 두개의 index로 substring의 시작점과 끝점을 가르키게 하면, mxn 매트릭스를 구성할 수 있다. 매트릭스의 원소는, substring이 palindromic 할 경우 그 substring의 길이를 넣어준다. 매트릭스를 채우고나서 최대 원소를 구하면 됨. $\rightarrow$ $O(n^2)$ time, $O(n^2)$ space
  • 비슷한 문제: LeetCode647. Panlidromic Substrings

Word Break

하나의 문자열과, 여러 단어가 들어있는 dictionary를 받아서, dictionary 안에 있는 문자만으로 주어진 문자열을 만들 수 있는지 여부를 리턴

풀이 방법

  • Brute force
    • n 개 문자로 이뤄진 문자열은, 최대 n-1개의 splitter로 쪼갤 수 있고 그 방법은 $2^{n-1}$ 개이 있고, word matching 하는 시도 횟수 n번을 곱하면 $O(n\times 2^{n-1})$ time complexity. 너무 심함 ㅠ
  • 일단 배열로 주어진 dictionary를 hashset으로 바꿔주자
    • 그러면, 해당 단어가 있는지를 $O(1)$에 판단할 수 있음.
  • 주어진 문장을 한번에 두개로 자르는 함수 WordBreak를 생각해보자
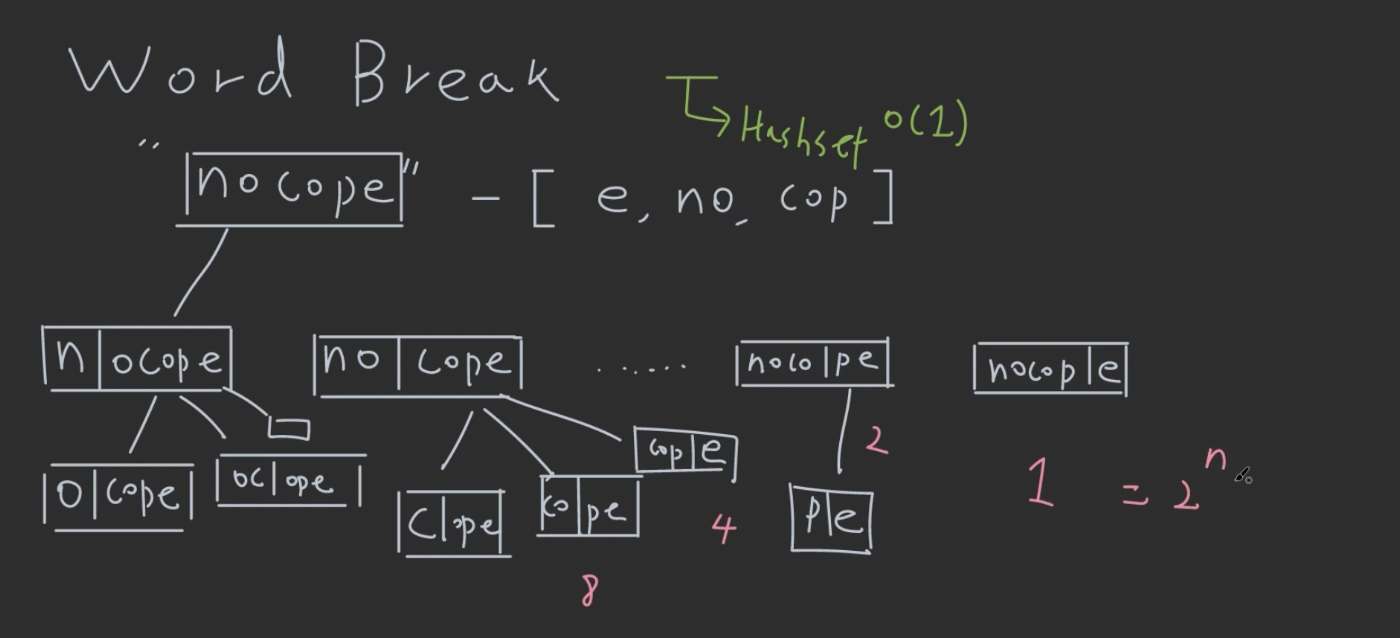
    • 한 번만 자르면, “nocope”를 “n”와 “ocope”, “no”와 “cope” 이런 식으로 나눌 수 있음.
    • 이렇게 만든 피라미드에 있는 node의 갯수, 즉 문장을 쪼개는 방법의 갯수는 $2^n$ (1+2+4+8 ….)
    • 첫 칸을 검색해서 hashset에 있으면 두번째 칸은 추가로 자르면서 recursive하게 진행해보면,
    • WB(“nocope”) =
      • WB(“ocope”)&&Dict(“n”)) WB(“cope”) && Dict(“no”)

  • 쪼개고 한 부분을 검색에서 찾으면, 남은 부분 쪼개고 다시 한 부분 검색 하는 방식으로 recursion 하면 됨.
  • 이 때 한 단계씩 깊어질 때마다 O(1)의 공간이 필요해서, 필요한 space complexity = O(n)

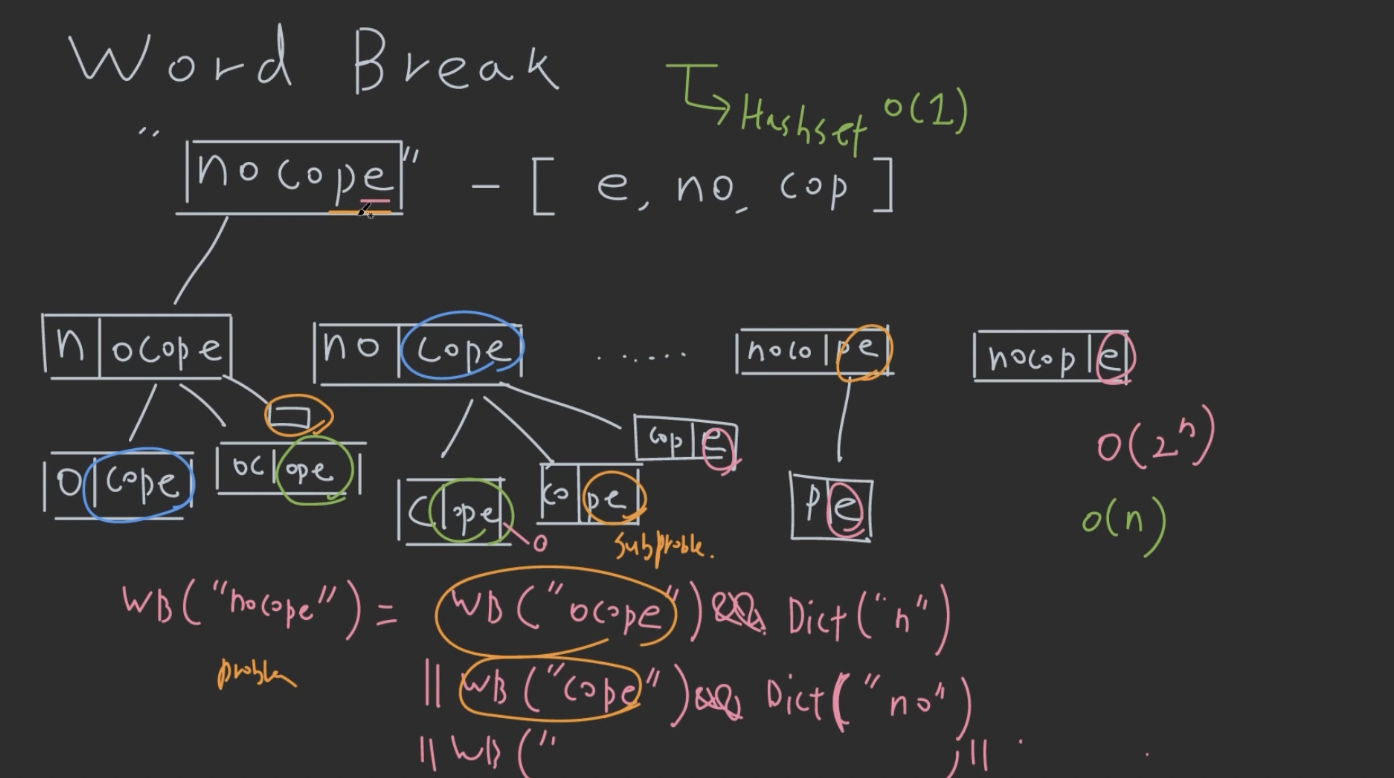
  • WB(“cope”)가 겹치는 거처럼 같은 subproblem을 반복해서 풀어야 하기 때문에, Memoization 해서 문제 더 빨리 풀 수 있음.
  • Bottom-up으로 해보자
    • 맨 뒤에 부터 한 글자 e, 두 글자 pe, 세 글자 ope, 이런 식으로 subproblem 등록해 놓을 수 있음
    • string의 글자 수와 같은 크기의 배열 WB를 만들고
    • WB(“pe”) 같은 뒤에서 두글자 경우의 결과를 WB의 뒤에서 두번째 자리에 배치

  • WB 배열을 왼쪽에서 채워나가는 방식으로 다시 풀면 …
    • empty string을 표현하는 칸을 배열 WB 맨 앞에 추가
    • n번째 칸의 결과는
      • n번째 칸의 위치에서 테스트하는 딕셔너리 단어의 길이만큼 앞에 있는 칸이 True이고
      • 그 사이의 글자들의 테스트하는 딕셔너리 단어와 동일할 때 True로 등록할 수 있음.

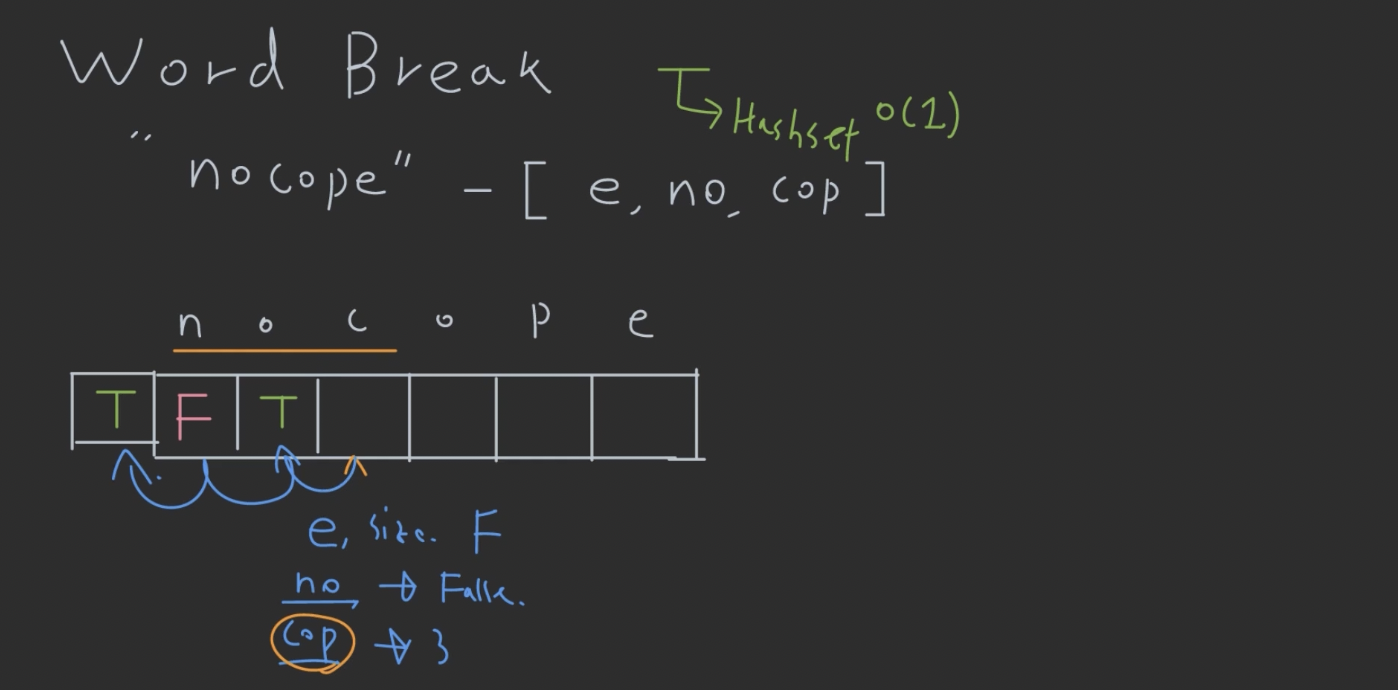
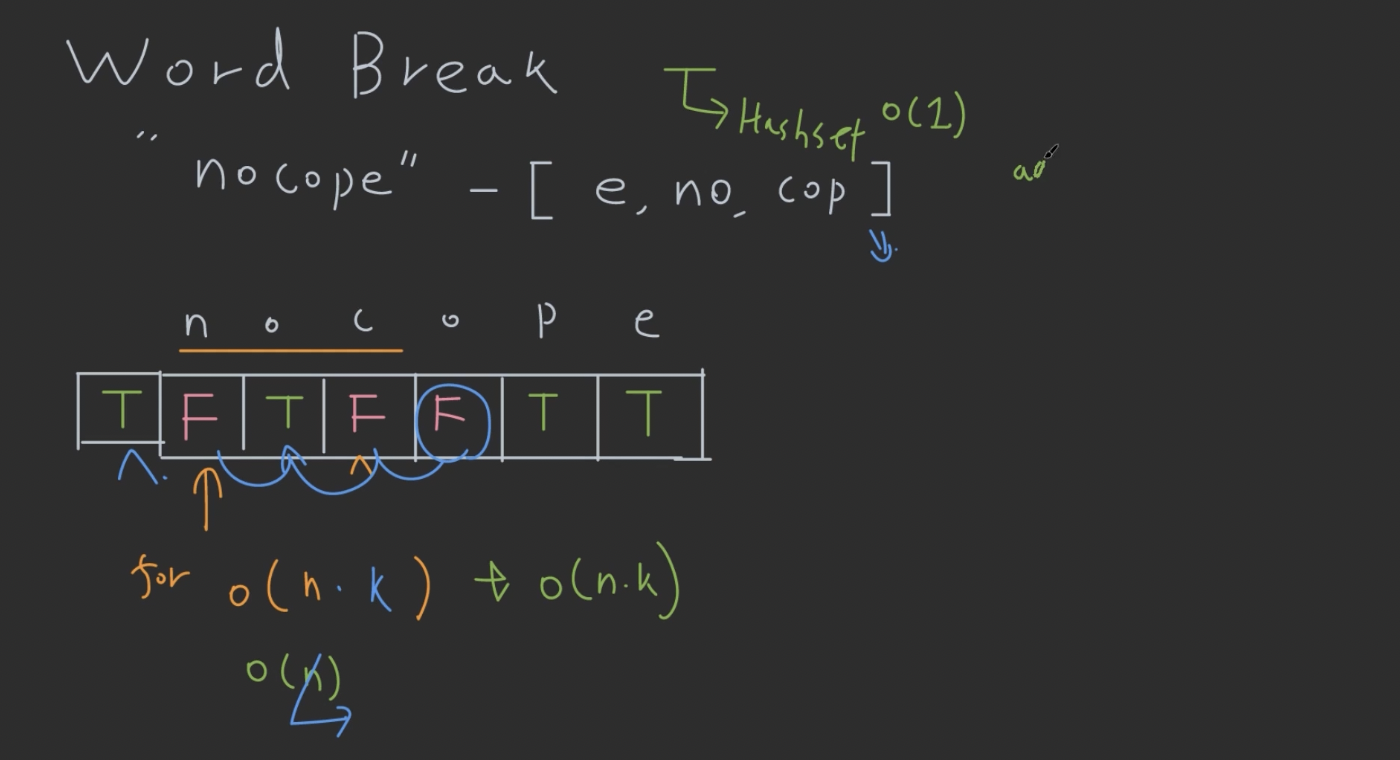
  • Add-on 문제: 딕셔너리 크기 K가 너무 크면??
    • string을 움직이는 포인터 2개 만들어서
    • 이중 for 문 만들고,
    • LP와 RP의 사이에 있는 substring이 딕셔너리 안에 있는가? 체크하면 됨
    • 그러면 $O(n\times k)$에서 $O(n^2)$ 로 크기가 작아짐.

0-1 Knapsack Problem

무게 제한 있는 가방에, 무게와 value가 정해져 있는 아이템을 여러 개 넣을 수 있는데, 이때 넣을 수 있는 최대 value를 구하기

풀이방법:

  • Brute-force:
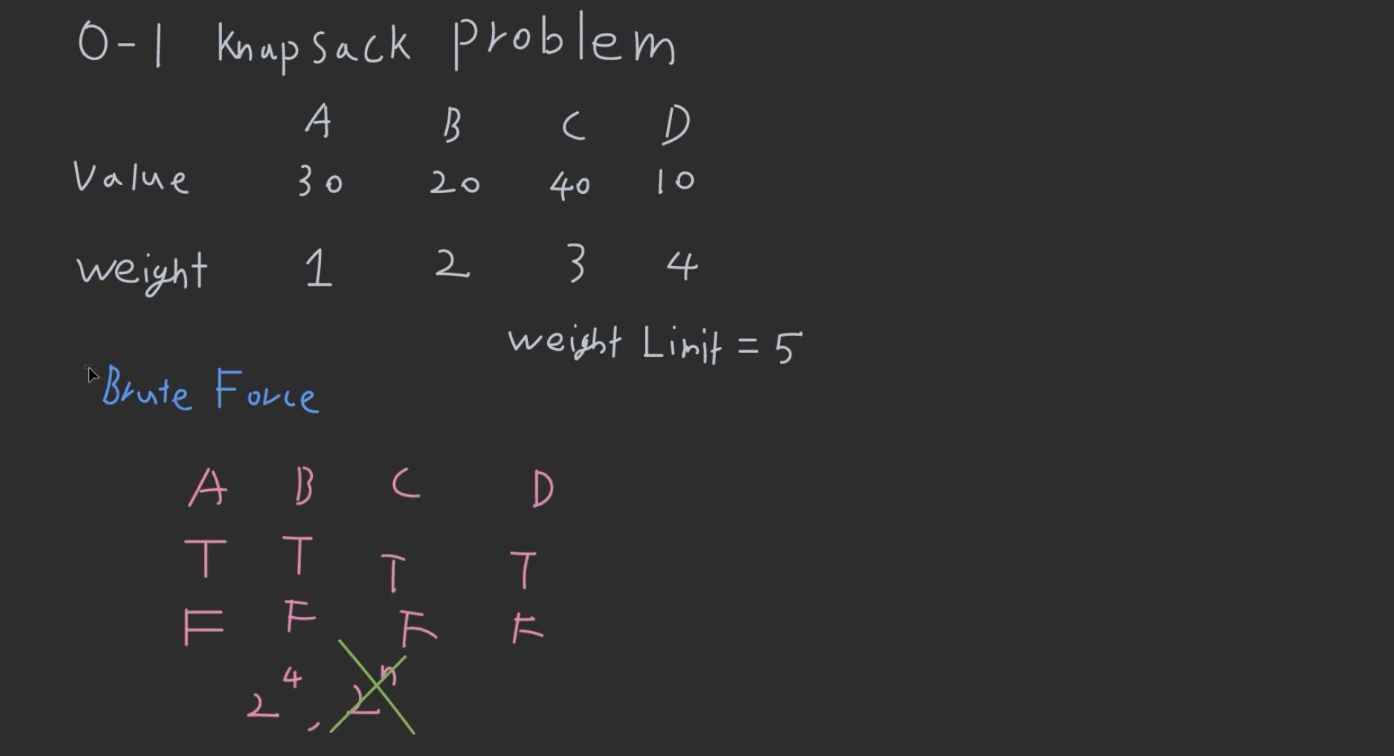
    • 4개의 item 있으면, $2^4$ 경우의 수 $\rightarrow$ $O(2^n)$
  • 최적화 문제니깐 Dynamic programming 의심해보자
    • Problem과 subproblem으로 쪼갤 수 있는가?
    • NS("ABCD",5)를 쪼개려면 ?
  • 잘못된 문제 쪼개기
    • 첫번째 arg는 sack에 넣을 후보 아이템들 (이미 넣었거나, 넣지 않기로 결정한 경우에는 여기서 배제 됨)
    • 두번째 arg는 sack의 남은 무게
    • 아래 그림의 네 가지 경우는 a, b, c, d를 하나씩 가방에 넣은 경우.
    • 하지만 이러면 아무것도 넣지 않는 경우를 놓치게 됨.
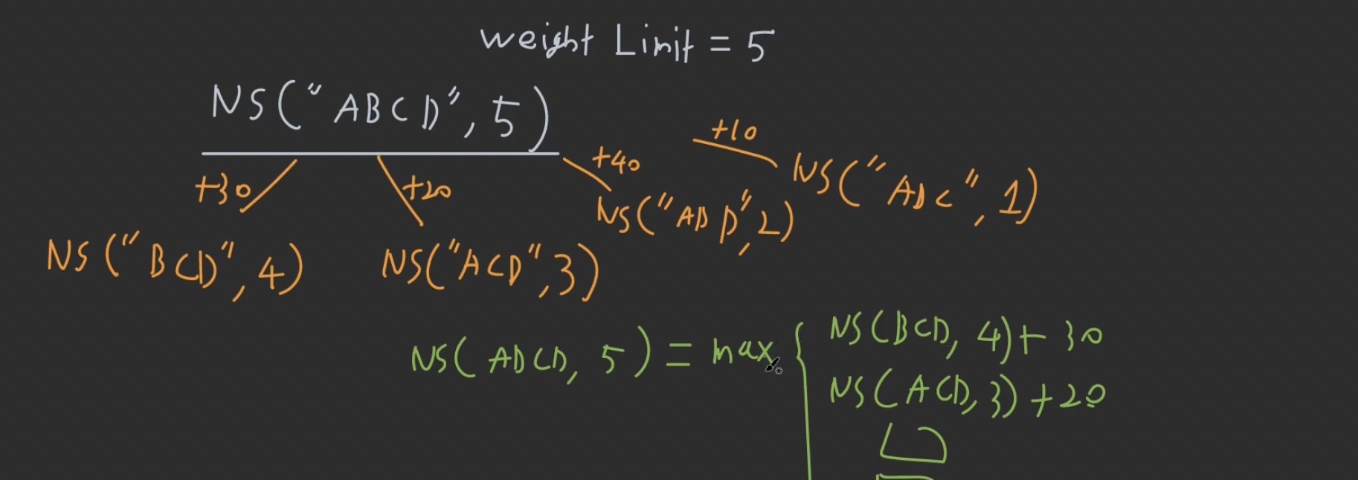
  • 제대로 쪼개기?!
    • 각 물체가 가방안에 있는 경우와 없는 경우를 고려해서 쪼개야 함
    • NS(n, w) 로 두개의 argument가 들어가니깐, 2차원 subproblem matrix를 만들어서 결과 저장해야 함

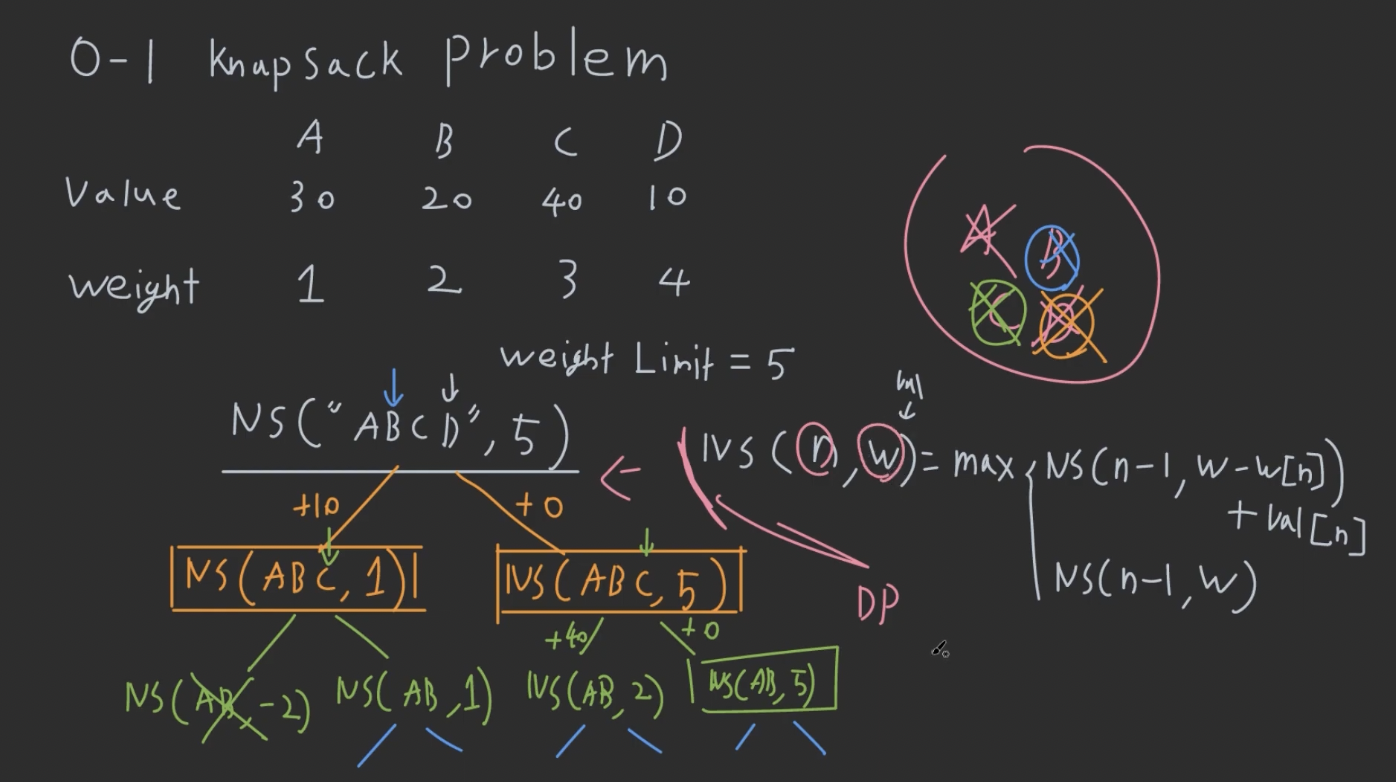
  • Top-down으로 풀기
    • NS(“ABCD”,5)에서 시작해서 초록색 링크 타고 갔다가,
    • 오렌지색 링크 타면서 값 만들기
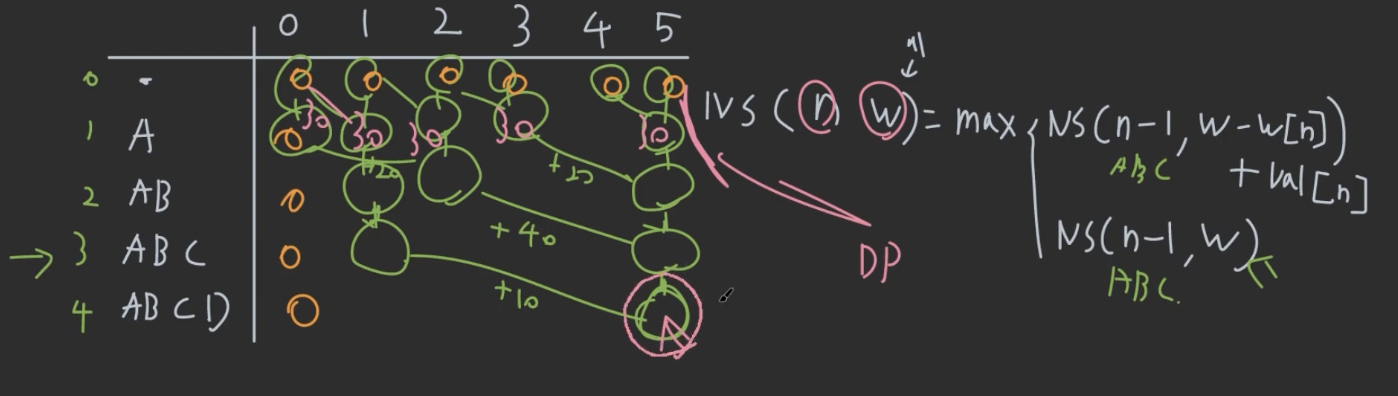
  • Bottom-up으로 풀기
    • 엣지에 있는 숫자로부터 매트릭스 채워나가기

  • Time complexity = $O(n\times w)$
  • Time complexity = $O(n\times w)$
    • $\rightarrow$ $O(w)$ 로 최적화 가능 (계산할 때 윗줄만 필요하니깐)

Partition Equal Subset Sum

주어진 배열을 두개의 subset으로 나눠서, 각 subset의 합이 같아지는 경우가 존재하는지를 리턴

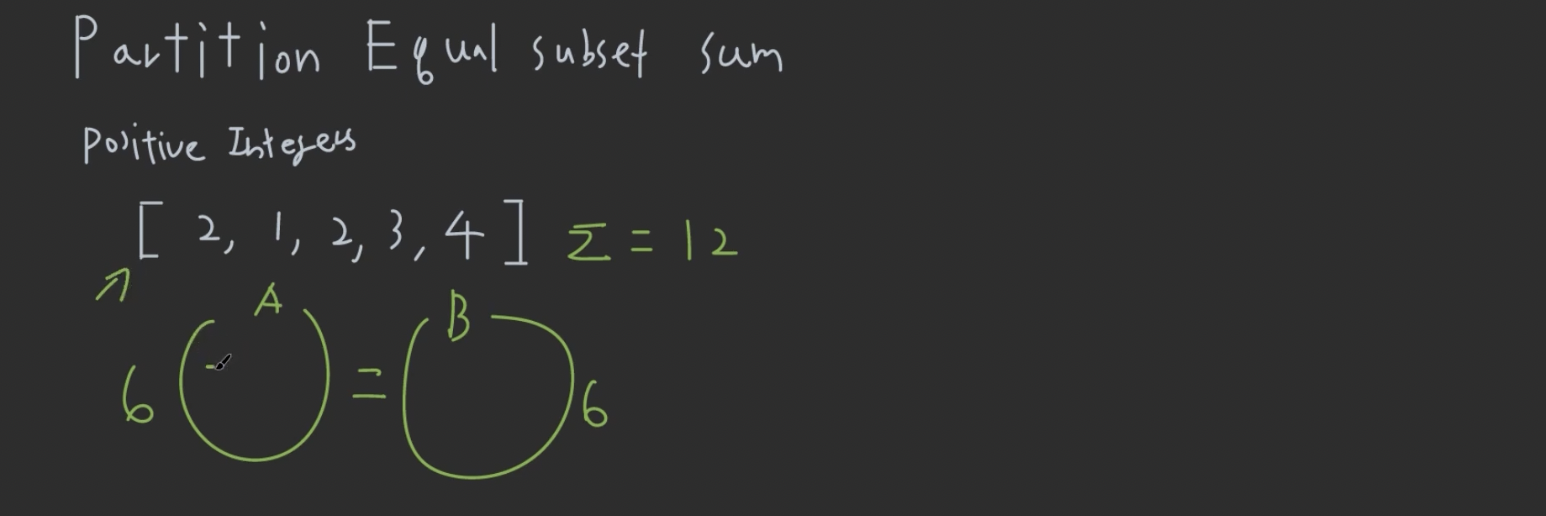
풀이방법

  • Brute-force:
    • 각 숫자가 첫번째 그룹에 선택 될 수 있고 안될 수 있으니깐.
    • $2^N$ complexity 갖는 문제
  • Problem과 Subproblem으로 나누기?
    • Knapsack 문제처럼,
    • 각 숫자가 첫번째 그룹 A에 포함될지 안될지 정하면 됨
    • 왼쪽은 맨 끝자리 수가 A에 포함되는 경우, 오른쪽은 포함 안되는 경우 (자동으로 B에 포함되는 경우)
    • DP(n,s) 를 저장하기 위한 2차원 배열 만들어서 채워나가면 문제 풀 수 있음

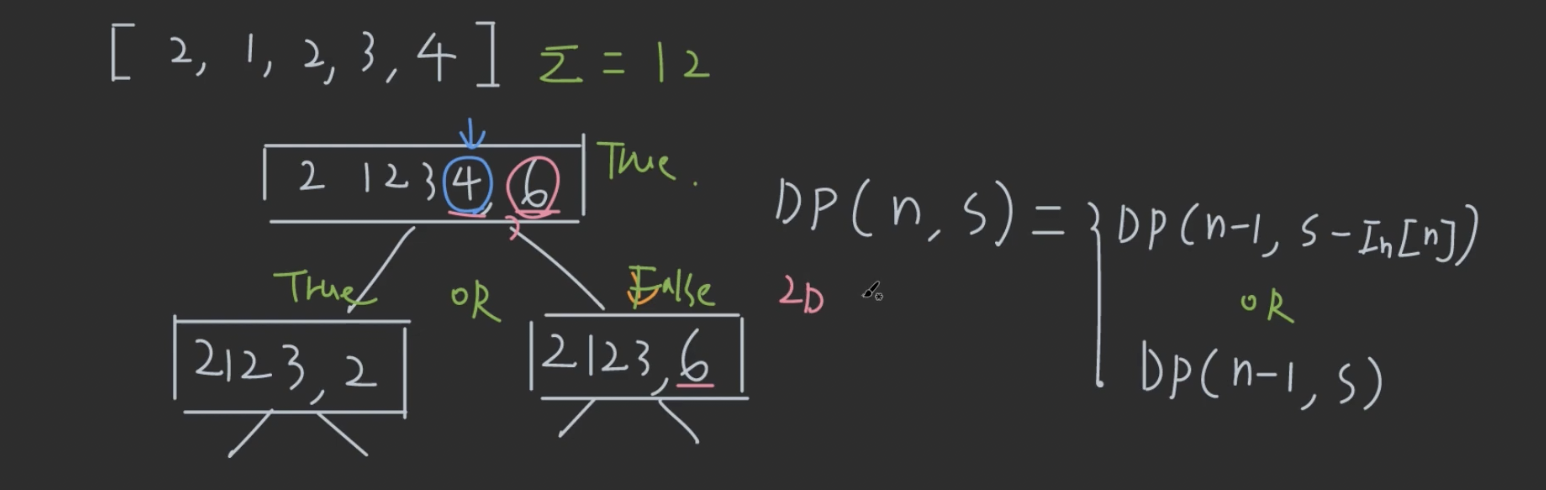
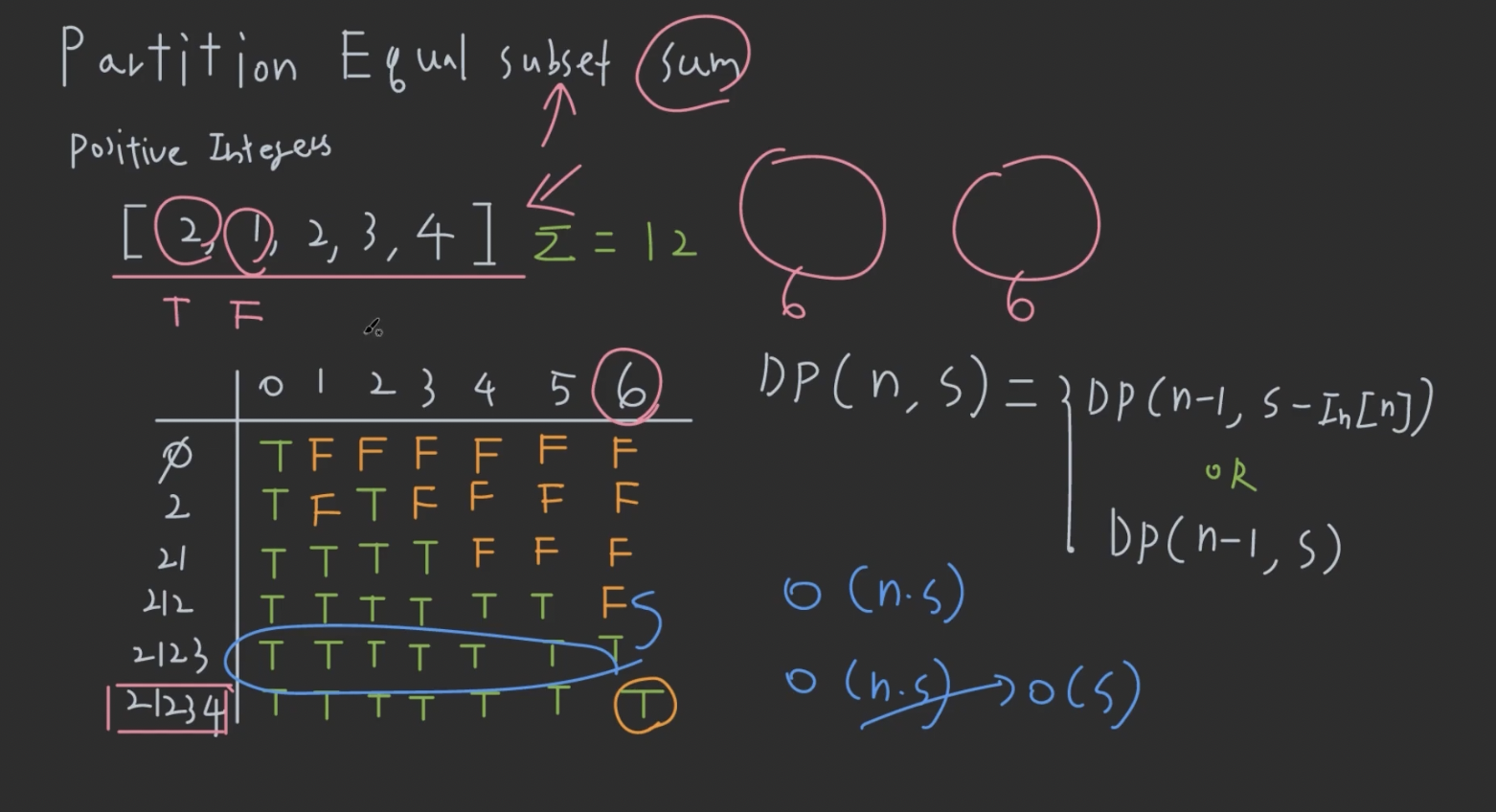
Coin Change II

동전의 종류가 주어지고, 동전으로 만들어야 할 target sum 주어지고, 각 동전은 무한개 가져다 쓸 수 있을 때, target sum 만들 수 있는지 여부 리턴

풀이방법:

  • 잘못된 문제나누기
    • 아래 그림은 동전이 선택되지 않는 경우가 포함 안 되어있음

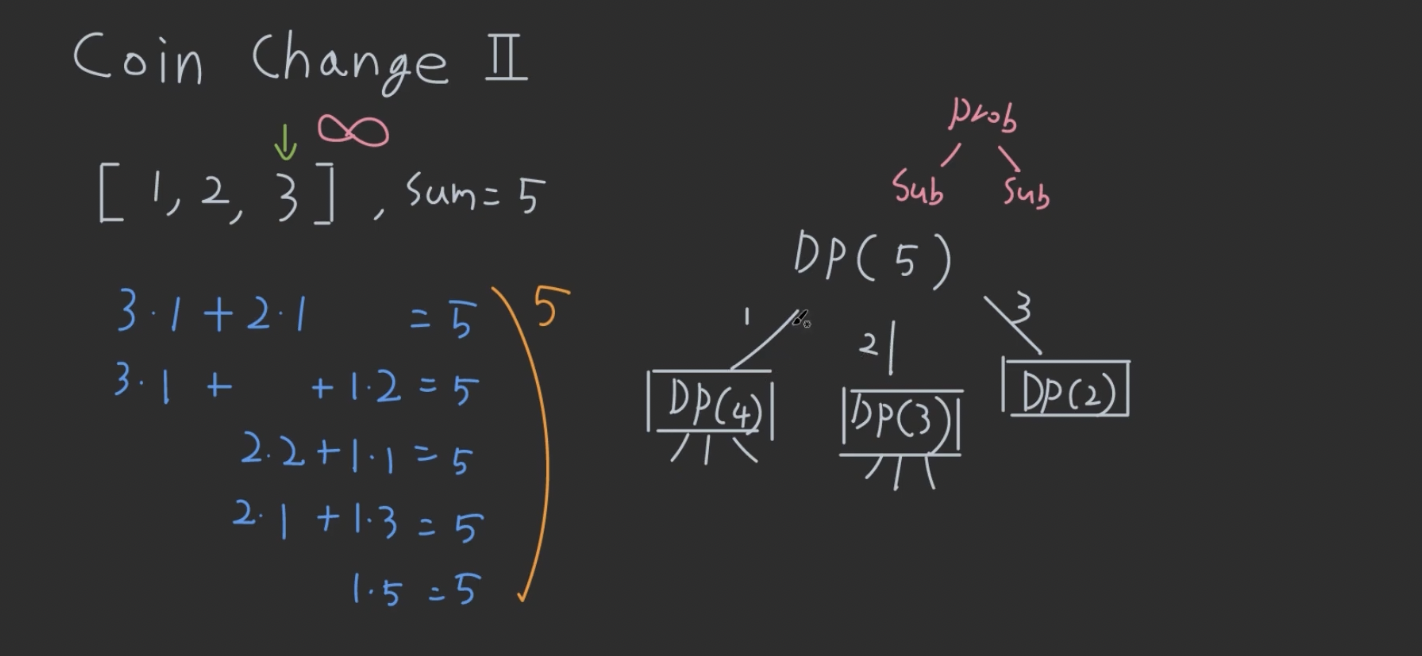
  • Knapsack처럼 동전을 포함할지 정해야 할 뿐만 아니라, 각 동전의 갯수까지 정해야하는 Knapsack 응용문제
    • 왼쪽은 마지막 숫자가 선택이 안 되었을 경우, 남은 sum은 그대로 5
    • 오른쪽은 선택이 되었을 경우, 선택된 3만큼 sum이 소비된 2가 남은 sum.
    • 코인 3을 중복 선택할 수 있으니, 첫번째 arg의 배열에서 3을 지우지 않기! : 이부분이 Knapsack과의 차이점!!

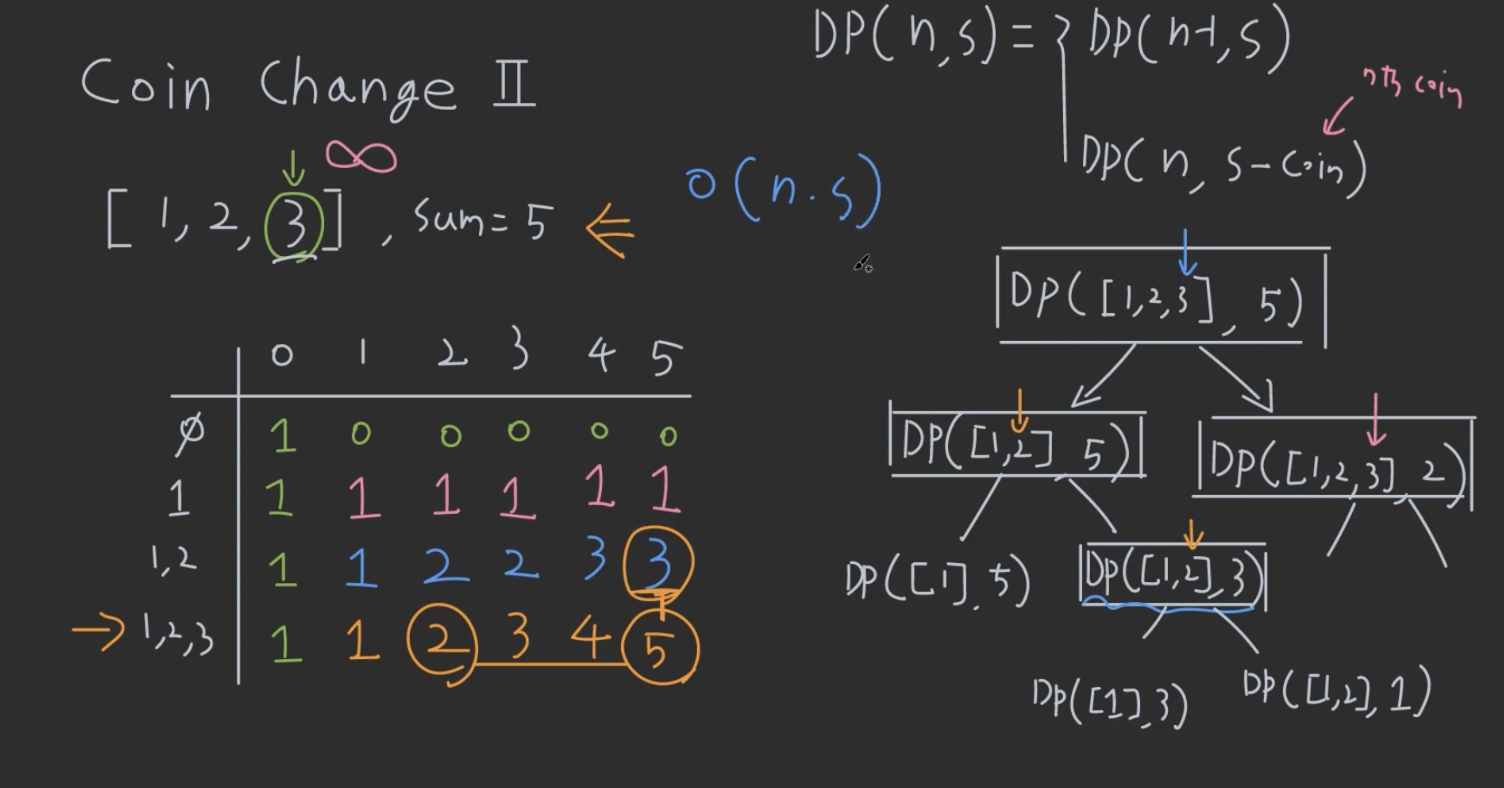
Reference

Notes Mentioning This Note

Data Structure and Algorithm Problems
Data Structure and Algorithm Problems

Table of Contents
Share on: